ELS는 이색옵션들이 결합된 상품이다. 특히 인기 많은 Step Down ELS는 행사가가 계속 바뀌는 디지털 옵션과 낙인이 발생하면 풋옵션이 생기는 배리어 옵션의 결합이다. 이런 복잡한 상품의 가격은 어떻게 평가할 수 있을까? ELS 평가 방법은 크게 2가지로 나뉜다. 바로 몬테카를로 시뮬레이션과 유한차분법(Finite Difference Method)이다.
몬테카를로 시뮬레이션 방식은 간단하다는 장점이 있으나 민감도의 안정도면에서는 단점이 있다. 간단한 바닐라옵션 같은 경우는 몬테카를로 시뮬레이션 방법으로도 괜찮으나 속도와 정확성을 요구하는 복잡한 이색옵션인 ELS 상품에게는 적합하지 않다. FDM은 어렵다는 단점이 있으나 민감도의 안정도면에서는 몬테카를로 방식보다 우수하다. 따라서, 업계에서는 주로 FDM을 통하여 ELS를 평가한다.
그럼, 유한차분법(FDM)에 대해 알아보자. FDM은 편미분방정식을 차분형태의 연립방정식으로 근사시키고, 연립방정식을 반복적으로 계산하여 해를 구하는 방법이다. FDM에는 명시적(Explicit) 방법, 암묵적(Implicit) 방법, 크랭크-니콜슨(Crank-Nicolson) 방법이 있다. 명시적 방법의 단점은 시간간격을 충분히 작게 하지 않으면 좋은 결과를 얻을 수 없다. 이러한 단점을 극복하기 위해 업계에서는 주로 암묵적 방법을 사용한다.
우선 기초자산이 1개인 상품의 가격 결정에 대해 알아보자. 블랙-숄즈 편미분방정식에 대해 아래의 그림과 같이 각 시점의 평가값을 이용하여 전 시점의 세 평가값을 추정하는 방법이 암묵적 방법이다. 이를 계속 반복하면 현재시점에서의 평가값을 구할 수 있다.

위 그림으로부터 다음과 같은 차분근사식을 유도한다.

그리고 대수정규분포를 적용한 블랙숄즈 편미분 방정식은 다음과 같다.

각 차분근사식을 블랙-숄즈 편미분방정식에 대입하여 정리하면 다음과 같이 나타낼 수 있다.

위의 차분 연립방정식은 바로 풀리지가 않는다. 따라서, 연립방정식에 경계조건을 적용해야한다. 경계조건(Boundary Conditions)에는 단말경계조건(Terminal BC)과 상하부경계조건(Upper and Lower BC)이 있다. 단말경계조건은 옵션만기 T시점에서 각 절점의 기초자산 수준에 따라 옵션의 손익을 부여하는 것이다. 여기서 유러피안 콜옵션일 경우에는 각 절점에서의 손익은 max(S-X, 0)이다. 상하부경계조건은 역행계산시 연립방정식을 이용하여 각 절점의 평가값을 구할 때 부족한 연립방정식 조건을 보완하기 위하여 최상부와 최하부에 경계조건을 부여하는 것이다.
단말경계조건으로 만기 시점의 옵션의 손익을 부여하여 위의 연립방정식을 이용하여 역행계산을 한다. 여기서 2M-1개의 값으로 1시점 전인 2M+1개의 값을 구하려면 2개의 추가적인 조건식이 필요하다. 추가적인 조건식은 최상부와 최하부 절점에 경계조건을 부여하여 얻을 수 있다.
그리고 최상부와 최하부 절점의 평가값을 정해주는 경계조건 부여 방법에는 델타값 입력, 감마값 입력 등의 방법이 있다. 델타값 입력 방법은 S가 충분히 클 때 콜옵션의 델타는 1, 충분히 작을 때는 0이라는 특성을 이용하는 것이고 제로감마컨디션이라고도 불리는 감마값 입력 방식은 ITM과 OTM에서 감마값은 0이라는 특성을 이용하는 것이다. 업계에서는 주로 제로감마컨디션을 사용한다.

차분격자 최상부 및 최하부 절점에 감마가 0인 경계조건은 다음과 같다.

이를 추가하여 삼중대각행렬 풀이법을 이용하여 연립방정식을 풀면 전 시점의 평가값을 구할 수 있다. 요약하면 단말경계조건에 의해 만기시점의 콜옵션의 가격을 계산하고 그 값에 제로감마컨디션을 이용하여 한 시점 앞으로 당기는 것을 현재시점까지 반복하면 현재시점의 옵션가격을 계산할 수 있다.
예시로 유러피안 콜옵션의 가치를 FDM과 블랙숄즈모형으로 계산하면 다음과 같다.

대부분의 ELS는 기초자산이 2개 이상이다. 지금부터 기초자산이 2개인 상품의 가격 결정에 대해 알아보자. 기초자산이 2개인 경우 암묵적 방법을 사용하면 연립방정식을 푸는데 시간이 너무 오래 걸린다. 따라서 ADI(Alternating Direction Implicit) 방법이나 OSM(Operator Splitting Method)와 같은 수치해석기법을 이용해야 한다. Greeks값이 비교적 안정적으로 계산된다고 알려진 OSM방법에 대해 알아보자.
기초자산들의 움직임에 대수정규분포를 적용하여 변수변환을 한, 기초자산이 2개인 블랙숄즈 편미분 방정식은 아래와 같다.


기초자산이 2개이기 때문에 역행계산을 한 시점을 두 시점으로 나누어 두 번 계산한다. 1단계 역행계산에서는 기초자산 1에 대해 계산하고 2단계 역행계산에서는 기초자산 2에 대해 계산한다.
위 편미분 방정식을 좌표변환 없이 tk+1시점에서 tk+0.5시점으로 1단계 역행계산 할 때에는 아래의 편미분 방정식을 적용하고,
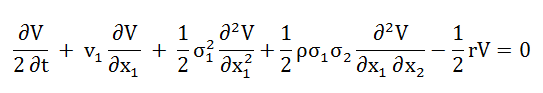
tk+0.5시점에서 tk시점으로 2단계 역행계산할 때에는 아래의 편미분 방정식을 적용한다.

1단계 역행계산 과정을 그림으로 표현해보면 다음과 같다.

1단계 역행계산의 편미분 방정식에 차분을 적용하여 정리하면 다음과 같다.

여기서, k+(1/2)시점의 미지수 3개는 삼중대각행렬 풀이법을 이용하면 구할 수 있다.
다음으로 2단계 역행계산 과정은 다음과 같다.

2단계 역행계산의 편미분 방정식에 차분을 적용하여 정리하면 다음과 같다.

여기서, k시점의 미지수 3개는 삼중대각행렬 풀이법을 이용하면 구할 수 있다
위의 1단계, 2단계 역행계산 과정을 평가시점까지 반복하면 평가시점에서 ELS의 가치를 계산할 수 있다.
'Finance > Derivatives' 카테고리의 다른 글
| [03. 옵션] 009. ELS(Equity Linked Securities)의 종류 (0) | 2019.10.14 |
|---|---|
| [03. 옵션] 008. 클리켓 옵션 or 래칫옵션(Cliquet Option or Ratchet Option) (0) | 2019.10.14 |
| [03. 옵션] 007. 아시안 옵션(Asian Option) (0) | 2019.10.14 |
| [03. 옵션] 006. 배리어 옵션(Barrier Option) (0) | 2019.10.13 |
| [03. 옵션] 005. 룩백 옵션(Lookback Option) (0) | 2019.10.13 |
 YOne Labs
YOne Labs



