다변량 페어트레이딩 모형의 식은 다음과 같다. 본 논문에서는 VAR(p)모형[1]을 사용한다.


1) Johansen Cointegration 방식
Johansen Cointegration Test는 VAR(Vector Autoregressive)모형을 기반으로 공적분 관계를 검정하고 공적분 계수를 구하는 방법론이다. Dickey-Fuller의 단위근 검정[2]을 다변량으로 확장한 것으로 보면 된다.
Engle과 Granger(1987)는 시계열 자료가 불안정하고 변수 간에 공적분 관계가 존재하면 이들 변수들 간의 관계는 오차수정모형(Error Correction Model)[3]으로 표현될 수 있다고 주장했다. 따라서 위 식을 벡터오차수정모형(Vector Error Correction Model)으로 변환시키면 다음과 같다.
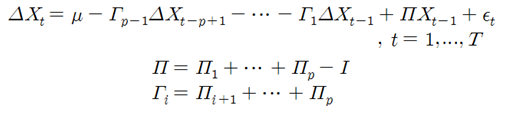
여기서 π의 Rank[4]가 0이면 의 모든 구성 시계열들은 단위근(비정상시계열)과정이 된다. 반면 π의 Rank가 n이면 Xt의 모든 구성 시계열들은 정상과정이 된다. 이때 π의 Rank가 0<r<n이면 r개의 Xt의 선형결합이 정상과정임을 뜻하고 이는 r개의 공적분 벡터를 가진다는 것을 의미한다. 이때 n개의 계열로 구성된 Xt간에 r개의 공적분 관계가 존재한다면 위 식의 π를 다음과 같이 다시 쓸 수 있다.
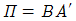
B는 적재벡터(loading vector) 또는 오차수정계수이며, A는 공적분 벡터이다.
이렇게 나온 공적분 벡터를 Trace Test나 Maximum Eigenvalue Test로 스프레드의 정상성을 검정한다. 여기에서는 Trace Test에 대해 알아보기로 한다.
2) 시차결정(p)
일변량 자기회귀모형(AR모형)에서는 시차를 PACF(Partial Autocorrelation Function)를 통해서 결정한다. 벡터자기회귀모형(VAR모형)에서는 일반적으로 AIC(Akaike Information Criterion) 또는 SIC(Schwarz Information Criterion)의 통계량을 최소화하는 방법으로 결정한다.

T는 데이터의 수, n은 시계열의 수, ∑p는 추정오차에 대한 공분산 행렬이다. 그리고 Hurvich와 Tsai(1993)은 수정된 AICc통계량을 제시했다.
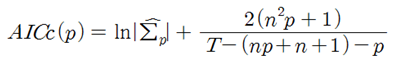
AICc는 p와 n이 늘어날수록 패널티를 부여한 방식이다.
3) Trace Test
Trace Test의 검정통계량은 다음과 같다.

귀무가설은 “공적분 벡터의 수가 r보다 작거나 같다”이다. 일반적으로 “공적분 관계가 0개이다”라는 귀무가설에서 시작하여 “공적분 관계가 1개이다”, “공적분 관계가 2개이다”, ··· , “공적분 관계가 n-1개이다”의 순서로 검정한다.
[1] 경제변수들간의 관계를 집약하는 방법론의 하나로 미국의 심스(Sims)를 위시한 통화론자들에 의해 개발되었다.
[2] 시계열의 정상성(stationary)을 검정하는 방법이다.
[3] 차분해서 안정화할 수 있는 불안정(non-stationary) 시계열들이더라도 선형결합은 안정적 확률과정이 될 수 있는 경우에
사용한다.
[4] 행렬의 행벡터 중 일차독립인 행벡터의 최대 개수를 말한다.
'Analysis > Market Neutral' 카테고리의 다른 글
| [01. Pairs Trading] 006. 다변량 페어트레이딩 모형 실습 (0) | 2019.10.21 |
|---|---|
| [01. Pairs Trading] 005. 이변량 페어트레이딩 모형 실습 (0) | 2019.10.21 |
| [01. Pairs Trading] 003. 페어트레이딩 모형 – 이변량 페어트레이딩 모형 (0) | 2019.10.20 |
| [01. Pairs Trading] 002. 페어트레이딩 전략의 구현 순서 (0) | 2019.10.19 |
| [01. Pairs Trading] 001. 페어트레이딩이란 (0) | 2019.10.19 |
 YOne Labs
YOne Labs



